Hacking Off

20% Time All the Time

EBNF to NFA for LR(0) and SLR(1) Grammars

This post is still somewhat incomplete.

LR(0) and SLR(1) grammars produce identical non-deterministic finite automata (NFA), and consequently, the same deterministic finite automata (DFA). However, they don’t produce the same tables.

Here’s how to build them.

How to construct the NFA for LR(0) and SLR(1) parser grammars

Augment the Grammar

Note: If the grammar’s leading non-terminal has only one production rule, skip this step.

Create a new production rule: Goal → YourOldStartingNonTerminal. E.g., convert A → ( A ) | a into:

  • A’ → A # This new production provides an unambiguous goal state.
  • A → ( A ) | a

Create the item list.

  1. First, rewrite the grammar as having one production rule per line. Using the above grammar, we get:

    • A’ → A # rule 1
    • A → ( A ) # rule 2
    • A → a # rule 3

  2. Next, “walk the dot.” For each production rule, transcribe it:

    • with a dot before the first symbol
    • with a dot before the second symbol
    • …
    • with a dot before the last symbol
    • with a dot after the last symbol

    The resulting item list grows rapidly. Using our example from above, we get the following:

    • A’ → • A # from rule 1
    • A’ → A • # from rule 1
    • A → • ( A ) # from rule 2
    • A → ( • A ) # from rule 2
    • A → ( A • ) # from rule 2
    • A → ( A ) • # from rule 2
    • A → • a # from rule 3
    • A → a • # from rule 3

Build the NFA Using the Item List

Quick definition: the current symbol is the symbol following the • marker.

  1. Draw a state containing the initial (goal) item.

  2. Draw a transition from State 0 on current symbol to State 1. (In our example, this means drawing an edge, labeled A, from the 1st item to the 2nd. It would look something like this:

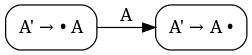
    Initial Parse State Finite Automata

  3. For each remaining item:

    1. IF the current symbol is non-terminal, draw ε-edges to the initial states for that symbol.
    2. Transition on the current symbol from the current state to the item in which the • marker has advanced past that symbol.

Next Time, Gadget! Next Time!

Next planned post on this subject: NFA to Table for LR(0) and SLR(1) Grammars

Glossary

  • Initial states for a non-terminal symbol P are states containing items such that:
    1. P is the left-hand-side of the production rule
    2. The • marker is left of all symbols in the production rule.

    For example: the initial states for A in the above grammar are:

    • A → • ( A )
    • A → • a